Wednesday, July 25, 2012

Conical spiral

This is a basic equation for a conical spiral.  

The conical spiral with angular frequency a on a cone of height h and radius r is a space curve given by the parametric equations
x=(h-z)/hrcos(az)
(1)
y=(h-z)/hrsin(az)
(2)
z=z.
(3)
The general form has parametric equations
x=trcos(at)
(4)
y=trsin(at)
(5)
z=t.
(6)
This curve has arc length function, curvature, and torsion given by
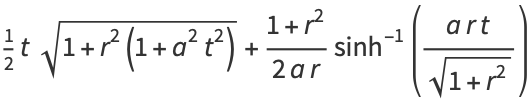s(t)=1/2tsqrt(1+r^2(1+a^2t^2))+(1+r^2)/(2ar)sinh^(-1)((art)/(sqrt(1+r^2)))
(7)
kappa(t)=(arsqrt(4+a^2t^2+r^2(2+a^2t^2)^2))/([1+r^2(1+a^2t^2)]^(3/2))
(8)
phi(t)=(a(6+a^2t^2))/(4+a^2t^2+r^2(2+a^2t^2)^2).





I like to dumb it down and call it my life being trapped in time.

Sorry an odd thought but one I couldn't get out of my mind today. You spiral down or you spiral up. No end in sight.










                                                                                                                             
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)